1D TV Denosing using Condat Algorithm#
import numpy as np
import math
import matplotlib.pyplot as plt
from scipy.sparse import csr_matrix, spdiags, diags, csc_matrix
from scipy.sparse.linalg import spsolve
from scipy.fftpack import fft, ifft
import time
import cv2
import urllib.request
from skimage.metrics import peak_signal_noise_ratio as PSNR
def TV_Condat_v2(y, lam):
start = time.time()
N = len(y)
if N <= 1:
return y
x = np.zeros_like(y)
cost = np.zeros(N)
indstart_low = np.zeros(N, dtype=int)
indstart_up = np.zeros(N, dtype=int)
j_low = j_up = jseg = indjseg = 0
indstart_low[0] = indstart_up[0] = 0
x_low_first = y[0] - lam
x_up_first = y[0] + lam
x_low_curr = x_low_first
x_up_curr = x_up_first
cost[0] = 0.5 * np.sum(np.abs(x - y) ** 2) + lam * np.sum(np.abs(np.diff(x)))
for i in range(1, N - 1):
if y[i] >= x_low_curr:
if y[i] <= x_up_curr:
x_up_curr = x_up_curr + (y[i] - x_up_curr) / (i - indstart_up[j_up] + 1)
x[indjseg] = x_up_first
while j_up > jseg and x_up_curr <= x[indstart_up[j_up - 1]]:
j_up -= 1
x_up_curr = x[indstart_up[j_up]] + (
x_up_curr - x[indstart_up[j_up]]
) * ((i - indstart_up[j_up + 1] + 1) / (i - indstart_up[j_up] + 1))
if j_up == jseg:
while x_up_curr <= x_low_first and jseg < j_low:
jseg += 1
x[indjseg : indstart_low[jseg] - 1] = x_low_first
x_up_curr = x_up_curr + (x_up_curr - x_low_first) * (
(indstart_low[jseg] - indjseg)
/ (i - indstart_low[jseg] + 1)
)
indjseg = indstart_low[jseg]
x_low_first = x[indjseg]
x_up_first = x_up_curr
j_up = jseg
indstart_up[jseg] = indjseg
else:
x[indstart_up[j_up]] = x_up_curr
else:
j_up += 1
indstart_up[j_up] = i
x[i] = y[i]
x_up_curr = x[i]
x_low_curr = x_low_curr + (y[i] - x_low_curr) / (
i - indstart_low[j_low] + 1
)
x[indjseg] = x_low_first
while j_low > jseg and x_low_curr >= x[indstart_low[j_low - 1]]:
j_low -= 1
x_low_curr = x[indstart_low[j_low]] + (
x_low_curr - x[indstart_low[j_low]]
) * ((i - indstart_low[j_low + 1] + 1) / (i - indstart_low[j_low] + 1))
if j_low == jseg:
while x_low_curr >= x_up_first and jseg < j_up:
jseg += 1
x[indjseg : indstart_up[jseg] - 1] = x_up_first
x_low_curr = x_low_curr + (x_low_curr - x_up_first) * (
(indstart_up[jseg] - indjseg) / (i - indstart_up[jseg] + 1)
)
indjseg = indstart_up[jseg]
x_up_first = x[indjseg]
x_low_first = x_low_curr
j_low = jseg
indstart_low[jseg] = indjseg
if indjseg == i:
x_low_first = x_up_first - 2 * lam
else:
x[indstart_low[j_low]] = x_low_curr
else:
j_low = j_low + 1
indstart_low[j_low] = i
x[i] = y[i]
x_low_curr = x[i]
# fusion of x_up to keep it nondecreasing
x_up_curr = x_up_curr + (y[i] - x_up_curr) / (i - indstart_up[j_up] + 1)
x[indjseg] = x_up_first
while j_up > jseg and x_up_curr <= x[indstart_up[j_up - 1]]:
j_up = j_up - 1
x_up_curr = x[indstart_up[j_up]] + (
x_up_curr - x[indstart_up[j_up]]
) * ((i - indstart_up[j_up + 1] + 1) / (i - indstart_up[j_up] + 1))
if j_up == jseg:
# a jump in x downwards is possible
while x_up_curr <= x_low_first and jseg < j_low:
# validation of segments of x_low in x
jseg += 1
x[indjseg : indstart_low[jseg] - 1] = x_low_first
x_up_curr = x_up_curr + (x_up_curr - x_low_first) * (
(indstart_low[jseg] - indjseg) / (i - indstart_low[jseg] + 1)
)
indjseg = indstart_low[jseg]
x_low_first = x[indjseg]
x_up_first = x_up_curr
j_up = jseg
indstart_up[jseg] = indjseg
if indjseg == i:
# this part is not mandatory, it is a kind of reset to increase numerical robustness.
x_up_first = x_low_first + 2 * lam
else:
x[indstart_up[j_up]] = x_up_curr
cost[i] = 0.5 * np.sum(np.abs(x - y) ** 2) + lam * np.sum(np.abs(np.diff(x)))
i = N - 1
if y[i] + lam <= x_low_curr:
# the segments of x_low are validated
while jseg < j_low:
jseg += 1
x[indjseg : indstart_low[jseg] - 1] = x_low_first
indjseg = indstart_low[jseg]
x_low_first = x[indjseg]
x[indjseg : i - 1] = x_low_first
x[i] = y[i] + lam
elif y[i] - lam >= x_up_curr:
while jseg < j_up:
jseg += 1
x[indjseg : indstart_up[jseg] - 1] = x_up_first
indjseg = indstart_up[jseg]
x_up_first = x[indjseg]
x[indjseg : i - 1] = x_up_first
x[i] = y[i] - lam
else:
x_low_curr = x_low_curr + (y[i] + lam - x_low_curr) / (
i - indstart_low[j_low] + 1
)
x[indjseg] = x_low_first
while j_low > jseg and x_low_curr >= x[indstart_low[j_low - 1]]:
j_low -= 1
x_low_curr = x[indstart_low[j_low]] + (
x_low_curr - x[indstart_low[j_low]]
) * ((i - indstart_low[j_low + 1] + 1) / (i - indstart_low[j_low] + 1))
if j_low == jseg:
if x_up_first >= x_low_curr:
x[indjseg:i] = x_low_curr
else:
x_up_curr = x_up_curr + (y[i] - lam - x_up_curr) / (
i - indstart_up[j_up] + 1
)
x[indjseg] = x_up_first
while j_up > jseg and x_up_curr <= x[indstart_up[j_up - 1]]:
j_up = j_up - 1
x_up_curr = x[indstart_up[j_up]] + (
x_up_curr - x[indstart_up[j_up]]
) * ((i - indstart_up[j_up + 1] + 1) / (i - indstart_up[j_up] + 1))
x[indstart_up[j_up] : i] = x_up_curr
while jseg < j_up:
jseg = jseg + 1
x[indjseg : indstart_up[jseg] - 1] = x_up_first
indjseg = indstart_up[jseg]
x_up_first = x[indjseg]
else:
x[indstart_low[j_low] : i] = x_low_curr
while jseg < j_low:
jseg = jseg + 1
x[indjseg : indstart_low[jseg] - 1] = x_low_first
indjseg = indstart_low[jseg]
x_low_first = x[indjseg]
cost[N - 1] = 0.5 * np.sum(np.abs(x - y) ** 2) + lam * np.sum(np.abs(np.diff(x)))
end = time.time()
return x, cost, end - start
s = np.loadtxt(
"https://eeweb.engineering.nyu.edu/iselesni/lecture_notes/TVDmm/TVD_software/blocks.txt"
)
y = np.loadtxt(
"https://eeweb.engineering.nyu.edu/iselesni/lecture_notes/TVDmm/TVD_software/blocks_noisy.txt"
)
N = 256
# N : signal length
sigma = 0.5; # sigma : standard deviation of noise
fig, axs = plt.subplots(1, 2, figsize=(15, 5))
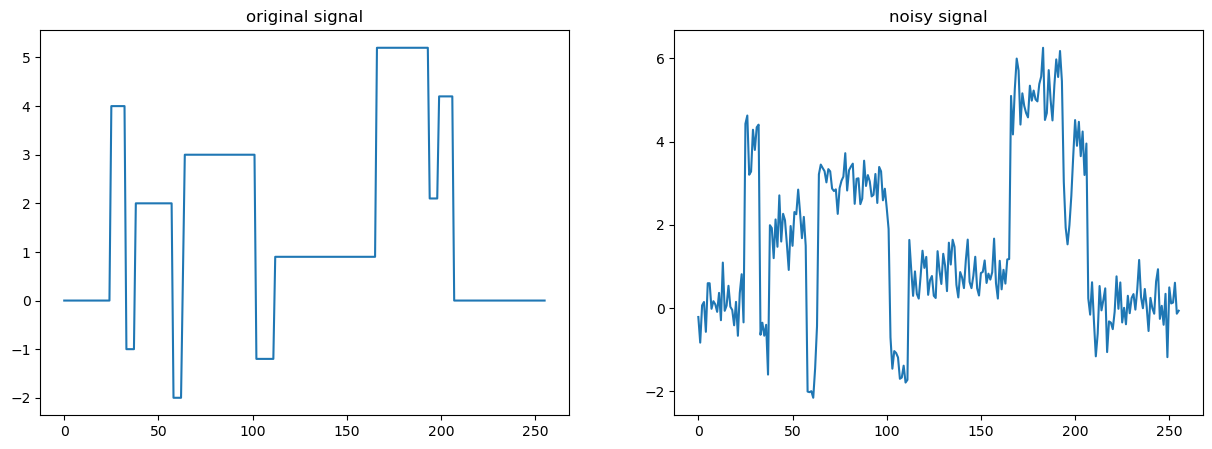
axs[0].plot(s)
axs[0].set_title("original signal")
axs[1].plot(y)
axs[1].set_title("noisy signal")
Text(0.5, 1.0, 'noisy signal')
lam = 3.0
x_condat, cost_condat, time_taken = TV_Condat_v2(y, lam)
fig, axs = plt.subplots(1, 4, figsize=(30, 5))
axs[0].plot(s)
axs[0].set_title("original signal")
axs[1].plot(y)
axs[1].set_title("noisy signal")
axs[2].plot(x_condat)
axs[2].set_title("recovered signal")
axs[3].plot(cost_condat)
axs[3].set_title("cost graph")
print(f"Time taken = {time_taken}")
Time taken = 0.007121562957763672

plt.plot(x_condat)
# plt.axis('off')
[<matplotlib.lines.Line2D at 0x7fb87685b4c0>]

def awgn(image, sigma_n):
noise = np.random.randn(image.shape[0], image.shape[1]) * sigma_n
return image + noise
def wrapper_condat(y):
img_, _, __ = TV_Condat_v2(y, lam)
return img_
def ADRA_algorithm(img):
rows_denoise = np.apply_along_axis(wrapper_condat, 0, img)
# cols_denoise = np.apply_along_axis(wrapper_condat, 1, img)
denoised = img.copy()
# Compute the adaptive weights
for i in range(0):
row_var = np.apply_along_axis(np.var, axis=1, arr=rows_denoise, ddof=1)
# col_var = np.apply_along_axis(np.var, axis=1, arr=cols_denoise, ddof=1)
# row_weight = 1 / (1 + row_var)
# col_weight = 1 / (1 + col_var)
# denoised = (rows_denoise * col_weight) + (cols_denoise * row_weight)
rows_denoise = np.apply_along_axis(wrapper_condat, 0, rows_denoise)
# cols_denoise = np.apply_along_axis(wrapper_condat, 1, cols_denoise)
return rows_denoise
url = "https://images.unsplash.com/photo-1664039591926-c1d776028289?ixlib=rb-4.0.3&ixid=MnwxMjA3fDB8MHxwaG90by1wYWdlfHx8fGVufDB8fHx8&auto=format&fit=crop&w=2022&q=80"
with urllib.request.urlopen(url) as url_response:
img_array = np.asarray(bytearray(url_response.read()), dtype=np.uint8)
img_gray = cv2.imdecode(img_array, cv2.IMREAD_GRAYSCALE)
img = cv2.resize(img_gray, (512, 512), interpolation=cv2.INTER_AREA)
img = img / img.max()
noisy_img = awgn(img, 0.1)
fig, axs = plt.subplots(1, 2, figsize=(15, 5))
axs[0].imshow(img, cmap="gray")
axs[0].set_title("original signal")
axs[1].imshow(noisy_img, cmap="gray")
axs[1].set_title("noisy signal")
Text(0.5, 1.0, 'noisy signal')

denoised_img = ADRA_algorithm(noisy_img)
fig, axs = plt.subplots(1, 4, figsize=(30, 5))
axs[0].imshow(img, cmap="gray")
axs[0].set_title("original signal")
axs[1].imshow(noisy_img, cmap="gray")
axs[1].set_title("noisy signal")
axs[2].imshow(denoised_img, cmap="gray")
axs[2].set_title("recovered signal")
# axs[3].plot(cost_condat)
# axs[3].set_title("cost graph")
# print(f"Time taken = {time_taken}")
print(f"noisy_img psnr = {PSNR(img.clip(0,1), noisy_img.clip(0,1))}")
print(f"noisy_img psnr = {PSNR(img.clip(0,1), denoised_img.clip(0,1))}")
noisy_img psnr = 20.806207490022338
noisy_img psnr = 19.316319415327502

def adra_1d(image):
# Initialize variables
x = np.copy(image)
s = np.copy(image)
gamma = 1.0
# Denoise rows
for j in range(image.shape[0]):
x[j, :] = wrapper_condat(x[j, :])
# Denoise columns
for k in range(image.shape[1]):
s[:, k] = wrapper_condat(s[:, k])
# Update x using ADRA formula
return s + x
denoised_img = adra_1d(noisy_img)
fig, axs = plt.subplots(1, 4, figsize=(30, 5))
axs[0].imshow(img, cmap="gray")
axs[0].set_title("original signal")
axs[1].imshow(noisy_img, cmap="gray")
axs[1].set_title("noisy signal")
axs[2].imshow(denoised_img, cmap="gray")
axs[2].set_title("recovered signal")
# axs[3].plot(cost_condat)
# axs[3].set_title("cost graph")
# print(f"Time taken = {time_taken}")
print(f"noisy_img psnr = {PSNR(img.clip(0,1), noisy_img.clip(0,1))}")
print(f"noisy_img psnr = {PSNR(img.clip(0,1), denoised_img.clip(0,1))}")
noisy_img psnr = 20.806207490022338
noisy_img psnr = 10.621736855646082
