TV Denoising with Adaptive learning rate

Import libraries

import numpy as np
import cv2
from matplotlib import pyplot as plt
import scipy.signal as signal
from scipy.signal import convolve2d
import scipy.fft as fft
import urllib.request
from skimage.metrics import peak_signal_noise_ratio as PSNR
import time

Import image

# Reading image (grayscale)
url = "https://i.stack.imgur.com/kP0u2.png"
# url='https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcSRsK5QFJ1arEQlnHEJ-020xbO30BgdYgPJBg&usqp=CAU'
# url='https://unsplash.com/photos/IoZA1Mwiq2g/download?ixid=MnwxMjA3fDB8MXxzZWFyY2h8MTZ8fGJsYWNrJTIwYW5kJTIwd2hpdGUlMjBmbG93ZXJ8ZW58MHx8fHwxNjc5MzQxODY4&force=true&w=640'
with urllib.request.urlopen(url) as url_response:
    img_array = np.asarray(bytearray(url_response.read()), dtype=np.uint8)
    img = cv2.imdecode(img_array, cv2.IMREAD_GRAYSCALE)
# img is a 3-dimensional numpy array (third number indicates channel)
# Converting to (0,1)
x = img.astype(float) / 255.0
print(type(img))
print(img.shape)
plt.imshow(x, cmap="gray")

<class 'numpy.ndarray'>
(512, 512)

<matplotlib.image.AxesImage at 0x7fb494c4e700>

Define conv and fft functions

# Define some of the operators that we need...
def conv2d_fft(x, h):
    p0 = x.shape[0] - h.shape[0]
    p1 = x.shape[1] - h.shape[1]
    h_pad = np.pad(h, ((0, p0), (0, p1)))
    Fh = fft.fft2(h_pad)
    Fx = fft.fft2(x)
    return np.real(fft.ifft2(Fx * Fh))


def conv2dT_fft(x, h):
    p0 = x.shape[0] - h.shape[0]
    p1 = x.shape[1] - h.shape[1]
    h_pad = np.pad(h, ((0, p0), (0, p1)))
    Fh = fft.fft2(h_pad)
    Fx = fft.fft2(x)
    return np.real(fft.ifft2(Fx * np.conj(Fh)))

Noise function

def awgn(img, n):
    """Generating Gaussian Noise
    with 0 mean and standard deviation n
    choose n between 0,1 for normalized image"""

    noise = np.random.randn(*img.shape) * n
    # Add the noise to the input image
    noisy_image = img + noise

    return noisy_image

Add noise to the image

"""
y1 = img + n
"""
# Add noise to the image
y1 = awgn(x, 0.4)

fig = plt.figure(figsize=(15, 15))
plt.subplot(121)
plt.imshow(x, cmap="gray", clim=[0, 1])
plt.title("image x")
plt.subplot(122)
plt.imshow(y1, cmap="gray", clim=[0, 1])
plt.title("Noisy image y = img + n")
plt.tight_layout()
plt.show()

Gradiant operator

# define gradient operators
"""
I am testing it with y1 for now
"""
dh = np.array([[1, -1], [0, 0]])  # horizontal gradient filter
dv = np.array([[1, 0], [-1, 0]])  # vertical gradient filter

Dh = lambda x: conv2d_fft(x, dh)
Dv = lambda x: conv2d_fft(x, dv)

DhT = lambda x: conv2dT_fft(x, dh)
DvT = lambda x: conv2dT_fft(x, dv)

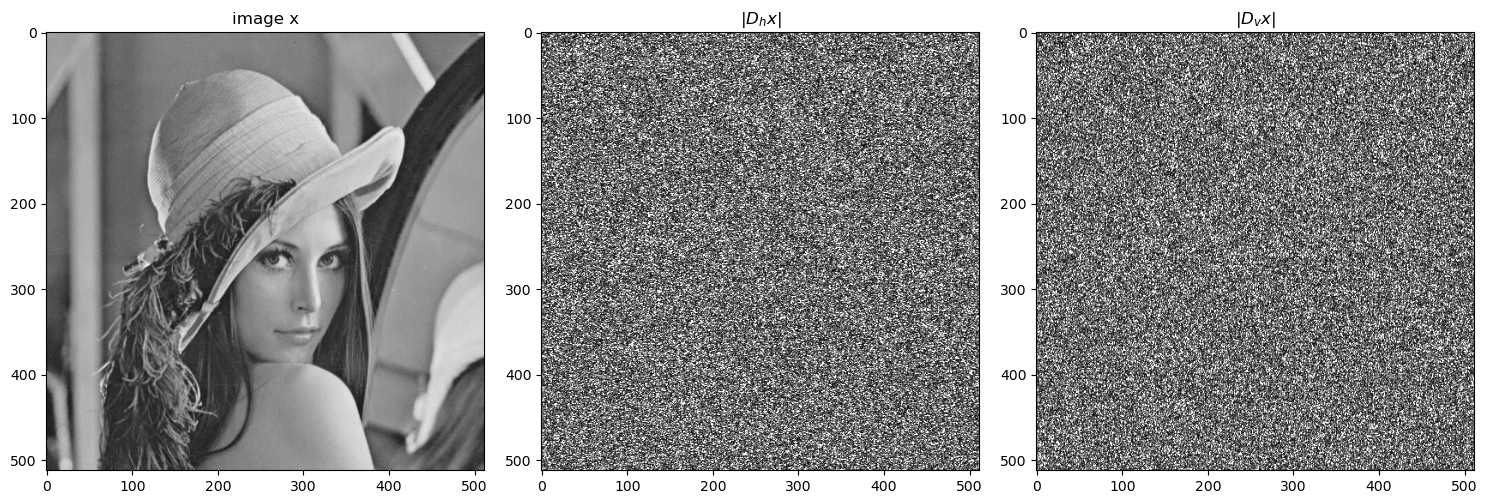
# plot the image x and the gradient images Dh x and Dv x
fig = plt.figure(figsize=(15, 15))
plt.subplot(131)
plt.imshow(x, cmap="gray", clim=[0, 1])
plt.title("image x")
plt.subplot(132)
plt.imshow(np.abs(Dh(y1)), cmap="gray", clim=[0, 1])
plt.title(r"$|D_hx|$")
plt.subplot(133)
plt.imshow(np.abs(Dv(y1)), cmap="gray", clim=[0, 1])
plt.title(r"$|D_vx|$")
plt.tight_layout()
plt.show()

class StepDecay:
    def __init__(self, initial_lr, drop_rate, epochs_per_drop):
        self.initial_lr = initial_lr
        self.drop_rate = drop_rate
        self.epochs_per_drop = epochs_per_drop

    def __call__(self, epoch):
        lr = self.initial_lr * self.drop_rate ** (
            np.floor(epoch / self.epochs_per_drop)
        )
        return lr

class ExpDecay:
    def __init__(self, initial_lr, decay_rate, decay_steps):
        self.initial_lr = initial_lr
        self.decay_rate = decay_rate
        self.decay_steps = decay_steps

    def __call__(self, epoch):
        lr = self.initial_lr * self.decay_rate ** (epoch / self.decay_steps)
        return lr

TV-denoising Solver

Write TV-denoising formulation with explanation here later

def TV_denoising(y, lamb=2, rho=1e1, maxiter=200, decay=None):
    """
    TV-denoising solver to solve
    minimize 0.5 |x-y|_2^2 + lambda|Dx|_1
    """
    # define the soft-thresholding function
    """
    In the TVD case we have : 
    Vector (v): Dx_(k+1) + u_(k)
    Threshold (t): lamb/rho
    """
    start = time.time()
    soft_thresh = lambda v, t: np.maximum(np.abs(v) - t, 0.0) * np.sign(v)

    # DDT
    """
        DDT = please check notes for fourier transform format
    """
    # Calculating the difference between sizes x and d for padding purpose
    p0 = x.shape[0] - dh.shape[0]
    p1 = x.shape[1] - dh.shape[1]
    dh_pad = np.pad(dh, ((0, p0), (0, p1)))

    p0 = x.shape[0] - dv.shape[0]
    p1 = x.shape[1] - dv.shape[1]
    dv_pad = np.pad(dv, ((0, p0), (0, p1)))

    # Refer to Parisima's notes for computing DDT using FFT
    DDT = np.abs(fft.fft2(dh_pad)) ** 2 + np.abs(fft.fft2(dv_pad)) ** 2

    # -----------------------------
    # initilize iteration variables
    zh = np.zeros_like(y)
    zv = np.zeros_like(y)
    uh = np.zeros_like(zh)
    uv = np.zeros_like(zv)
    x_hat = np.zeros_like(y)
    # For computing error
    J = np.zeros(maxiter)

    for k in range(maxiter):
        # solve the L2-L2 problem (update x)
        rhs = y + rho * (DhT(zh) + DvT(zv)) - DhT(uh) - DvT(uv)
        F_rhs = fft.fft2(rhs)
        x_hat = np.real(fft.ifft2(F_rhs / (rho * DDT + 1)))

        # solve the TV problem (update z)
        zh = soft_thresh(Dh(x_hat) + uh, lamb / rho)
        zv = soft_thresh(Dv(x_hat) + uv, lamb / rho)

        # update u
        dual_h = Dh(x_hat) - zh
        dual_v = Dv(x_hat) - zv
        uh = uh + dual_h
        uv = uv + dual_v

        # compute the error
        J[k] = (dual_h**2).sum() + (dual_v**2).sum()

        if decay is not None:
            lamb = decay(k)
    end = time.time()
    return x_hat, J, end - start

lamb = 0.5
maxiter = 100
rho = 2
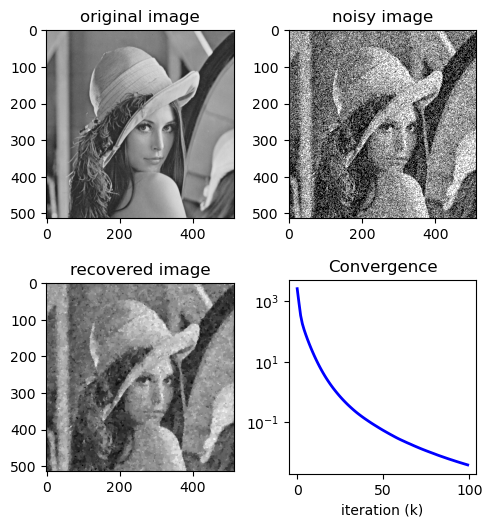
x_hat, J, duration = TV_denoising(y1, lamb=lamb, rho=rho, maxiter=maxiter, decay=None)

fig = plt.figure()
fig.set_size_inches(5, 7.5)
ax = fig.add_subplot(321)
ax.imshow(x, cmap="gray", clim=[0, 1])
plt.title("original image")
ax2 = fig.add_subplot(322)
ax2.imshow(y1, cmap="gray", clim=[0, 1])
plt.title("noisy image")
ax3 = fig.add_subplot(323)
ax3.imshow(x_hat, cmap="gray", clim=[0, 1])
plt.title("recovered image")
ax4 = fig.add_subplot(324)
ax4.semilogy(range(len(J)), J, "b-", lw=2)
plt.title("Convergence")
plt.xlabel("iteration (k)")
plt.tight_layout()
plt.show()
print(f"Time taken = {duration}")

Time taken = 15.130998134613037

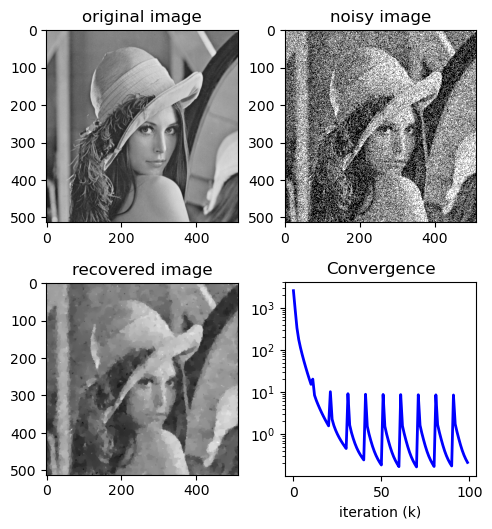
step_decay = StepDecay(initial_lr=lamb, drop_rate=1.03, epochs_per_drop=10)
x_hat_step, J_step, duration = TV_denoising(
    y1, lamb=lamb, rho=rho, maxiter=maxiter, decay=step_decay
)

fig = plt.figure()
fig.set_size_inches(5, 7.5)
ax = fig.add_subplot(321)
ax.imshow(x, cmap="gray", clim=[0, 1])
plt.title("original image")
ax2 = fig.add_subplot(322)
ax2.imshow(y1, cmap="gray", clim=[0, 1])
plt.title("noisy image")
ax3 = fig.add_subplot(323)
ax3.imshow(x_hat_step, cmap="gray", clim=[0, 1])
plt.title("recovered image")
ax4 = fig.add_subplot(324)
ax4.semilogy(range(len(J_step)), J_step, "b-", lw=2)
plt.title("Convergence")
plt.xlabel("iteration (k)")
plt.tight_layout()
plt.show()
print(f"Time taken = {duration}")

Time taken = 15.067909002304077

exp_decay = ExpDecay(initial_lr=lamb, decay_rate=1.03, decay_steps=10)
x_hat_exp, J_exp, duration = TV_denoising(
    y1, lamb=lamb, rho=rho, maxiter=maxiter, decay=exp_decay
)

fig = plt.figure()
fig.set_size_inches(5, 7.5)
ax = fig.add_subplot(321)
ax.imshow(x, cmap="gray", clim=[0, 1])
plt.title("original image")
ax2 = fig.add_subplot(322)
ax2.imshow(y1, cmap="gray", clim=[0, 1])
plt.title("noisy image")
ax3 = fig.add_subplot(323)
ax3.imshow(x_hat_exp, cmap="gray", clim=[0, 1])
plt.title("recovered image")
ax4 = fig.add_subplot(324)
ax4.semilogy(range(len(J_exp)), J_exp, "b-", lw=2)
plt.title("Convergence")
plt.xlabel("iteration (k)")
plt.tight_layout()
plt.show()
print(f"Time taken = {duration}")

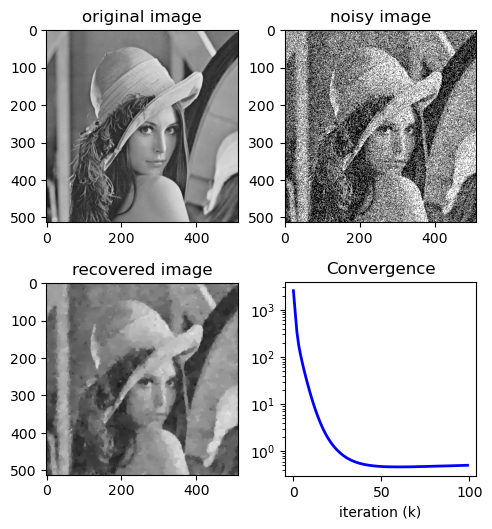
Time taken = 14.249502182006836

list_of_imgs = [x, y1, x_hat, x_hat_step, x_hat_step]
list_of_titles = [
    "original",
    "noisy",
    "TVD",
    "TVD with step decay",
    "TVD with exp decay",
]

fig = plt.figure(figsize=(20, 20))
for i, img in enumerate(list_of_imgs):
    plt.subplot(1, 7, i + 1)
    plt.axis("off")
    plt.imshow(img, cmap="gray", clim=[0, 1])
    plt.title(list_of_titles[i])

for i, img in enumerate(list_of_imgs[1:]):
    fig = plt.figure(figsize=(20, 20))
    plt.subplot(1, 7, 1)
    plt.title(list_of_titles[i + 1])
    plt.axis("off")
    plt.imshow(x, cmap="gray", clim=[0, 1])
    plt.subplot(1, 7, 2)
    plt.axis("off")
    plt.imshow(img, cmap="gray", clim=[0, 1])
    plt.title(f"PSNR = {PSNR(x.clip(0,1), img.clip(0,1)):.2f}")