1D TV Denoising algorithms#
Implementation of 1D TVD using Maximization and Minimization algorithm and Iterative clipping algorithm. Reference
import numpy as np
import math
import matplotlib.pyplot as plt
from scipy.sparse import csr_matrix, spdiags, diags, csc_matrix, eye
from scipy.sparse.linalg import spsolve
from scipy.linalg import solve
from scipy.fftpack import fft, ifft
import time
s = np.loadtxt(
"https://eeweb.engineering.nyu.edu/iselesni/lecture_notes/TVDmm/TVD_software/blocks.txt"
)
y = np.loadtxt(
"https://eeweb.engineering.nyu.edu/iselesni/lecture_notes/TVDmm/TVD_software/blocks_noisy.txt"
)
N = 256
# N : signal length
sigma = 0.5; # sigma : standard deviation of noise
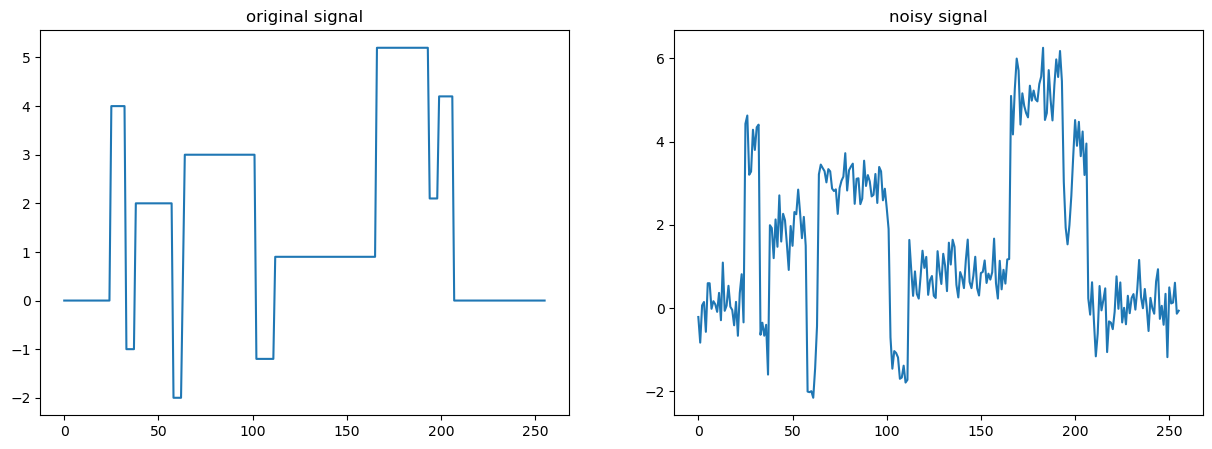
fig, axs = plt.subplots(1, 2, figsize=(15, 5))
axs[0].plot(s)
axs[0].set_title("original signal")
axs[1].plot(y)
axs[1].set_title("noisy signal")
Text(0.5, 1.0, 'noisy signal')
Using linear systems#
def tvd_mm(y, lam, Nit):
start = time.time()
# Cost function history
cost = np.zeros(Nit)
# Signal length
N = y.shape[0]
# Create sparse difference matrix
I = np.eye(N)
D = spdiags(np.vstack((np.ones((1, N)), -1 * np.ones((1, N)))), [0, 1], N - 1, N)
DDT = D @ D.T
# Initialization
x = y.copy()
Dx = D @ x
Dy = D @ y
for k in range(Nit):
# Compute banded matrix F
F = csc_matrix(diags(np.abs(Dx).flatten() / lam, 0)) + DDT
# Solve linear system to get updated signal x
x = y - D.T @ spsolve(F, Dy)
# Update variables
Dx = D @ x
cost[k] = 0.5 * np.sum(np.abs(x - y) ** 2) + lam * np.sum(np.abs(Dx))
end = time.time()
return x.flatten(), cost, end - start
lam = 1.5
max_iter = 256
x_mm, cost_mm, time_taken = tvd_mm(y, lam, max_iter)
fig, axs = plt.subplots(1, 4, figsize=(30, 5))
axs[0].plot(s)
axs[0].set_title("original signal")
axs[1].plot(y)
axs[1].set_title("noisy signal")
axs[2].plot(x_mm)
axs[2].set_title("recovered signal")
axs[3].plot(cost_mm)
axs[3].set_title("cost graph")
print(f"Time taken = {time_taken}")
Time taken = 0.2121448516845703

def tvd_ic(y, lam, Nit):
start = time.time()
y = y.reshape((1, -1)) # row vector
J = np.zeros(Nit) # objective function
N = y.shape[1]
z = np.zeros((1, N - 1))
alpha = 3
T = lam / 2
x = y.copy()
for k in range(Nit):
inter = np.concatenate((-z[:, 0], -np.diff(z.flatten()), z[:, -1]))
x = y - inter # y - D' z
J[k] = 0.5 * np.sum(np.abs(x - y) ** 2) + lam * np.sum(np.abs(np.diff(x)))
z = z + 1 / alpha * np.diff(x) # z + 1/alpha D z
z = np.clip(z, -T, T) # clip(z,T)
end = time.time()
return x.flatten(), J, end - start
max_iter = 256
x_ic, cost_ic, time_taken = tvd_ic(y, 1.5 * lam, max_iter)
fig, axs = plt.subplots(1, 4, figsize=(30, 5))
axs[0].plot(s)
axs[0].set_title("original signal")
axs[1].plot(y)
axs[1].set_title("noisy signal")
axs[2].plot(x_ic)
axs[2].set_title("recovered signal")
axs[3].plot(cost_ic)
axs[3].set_title("cost graph")
print(f"Time taken = {time_taken}")
Time taken = 0.019545793533325195

soft_thresh = lambda v, t: np.maximum(np.abs(v) - t, 0.0) * np.sign(v)
# def tvd_admm(y, lam, Nit, mu1=1, mu2=1):
# start = time.time()
# cost = np.zeros(Nit) # objective function
# print(y.shape)
# # Signal length
# N = y.shape[0]
# T = 0.5 * lam / mu2
# e = np.ones(N - 1)
# Dmtx = spdiags([e, -e], [0, 1], N - 1, N) # sparse matrix
# F = mu1 * eye(N) + mu2 * (Dmtx.T @ Dmtx) # sparse matrix
# D = lambda x: np.diff(x, axis=0) # D
# DT = lambda x: np.concatenate(([-x[0,:]], -np.diff(x, axis=0), [x[-1,:]])) # D'
# # initializations
# # u1 = y.copy()
# # d1 = np.zeros((N, 1))
# # u2 = np.zeros((N-1, 1))
# # d2 = np.zeros((N-1, 1))
# d = np.zeros((N-1, 1))
# x = np.zeros((N, 1))
# for k in range(Nit):
# u = soft_thresh(D(x) + d, T)
# x = spsolve(F, (y + mu2*DT(u-d)))
# d = d - (u - D(x))
# cost[k] = np.sum(np.abs(x - y) ** 2) + lam * np.sum(np.abs(D(x)))
# # for k in range(Nit):
# # v1 = (y - d1 + mu1 * x) / (1 + mu1)
# # v2 = soft_thresh(D(x)+d2, T) - d2
# # x = spsolve(F, mu1 * v1 + mu2 * DT(v2)) # sparse system solve
# # d1 = x - v1
# # d2 = D(x) - v2
# # cost[k] = np.sum(np.abs(x - y) ** 2) + lam * np.sum(np.abs(D(x)))
# # for k in range(Nit):
# # x = spsolve(F, (mu1*(u1-d1) + mu2*DT(u2-d2)))
# # u1 = (y + mu1*(x+d1)) / (1 + mu1)
# # u2 = soft_thresh(D(x)+d2, T)
# # d1 = d1 - (u1-x)
# # d2 = d2 - (u2-D(x))
# # cost[k] = np.sum(np.abs(x - y) ** 2) + lam * np.sum(np.abs(D(x)))
# end = time.time()
# return x.flatten(), cost, end-start
# ver3
def tvd_admm(y, lam, Nit, mu1=1, mu2=1):
start = time.time()
y = np.expand_dims(y, axis=1)
cost = np.zeros(Nit) # objective function
# Signal length
N = y.shape[0]
T = 0.5 * lam / mu2
e = np.ones(N - 1)
Dmtx = spdiags([e, -e], [0, 1], N - 1, N) # sparse matrix
F = mu1 * eye(N) + mu2 * (Dmtx.T @ Dmtx) # sparse matrix
print(F.shape)
D = lambda x: np.diff(x, axis=0) # D
DT = lambda x: np.concatenate((-x[:1,], -np.diff(x, axis=0), x[-1:,])) # D'
# initializations
# u1 = y.copy()
d1 = np.zeros((N, N))
d2 = np.zeros((N - 1, 1))
x = np.zeros((N, 1))
for k in range(Nit):
v1 = (y - d1 + mu1 * x) / (1 + mu1)
v2 = soft_thresh(D(x) + d2, T) - d2
x = spsolve(F, mu1 * v1 + mu2 * DT(v2)) # sparse system solve
d1 = x - v1
d2 = D(x) - v2
# x = np.expand_dims(x,axis=1)
cost[k] = np.sum(np.abs(x - y) ** 2) + lam * np.sum(np.abs(D(x)))
end = time.time()
return x.flatten(), cost, end - start
max_iter = 256
x_admm, cost_admm, time_taken = tvd_admm(y, lam, max_iter)
fig, axs = plt.subplots(1, 4, figsize=(30, 5))
axs[0].plot(s)
axs[0].set_title("original signal")
axs[1].plot(y)
axs[1].set_title("noisy signal")
axs[2].plot(x_admm)
axs[2].set_title("recovered signal")
axs[3].plot(cost_admm)
axs[3].set_title("cost graph")
print(f"Time taken = {time_taken}")
(256, 256)
Time taken = 1.1289477348327637

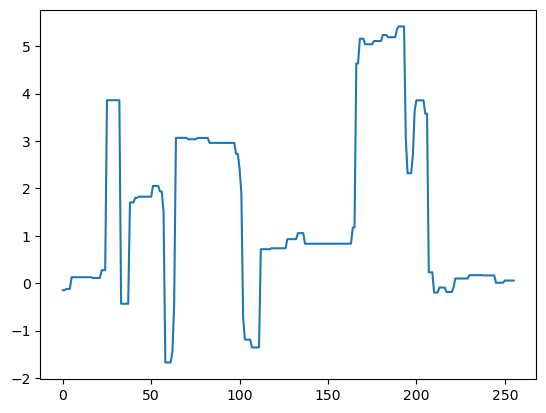
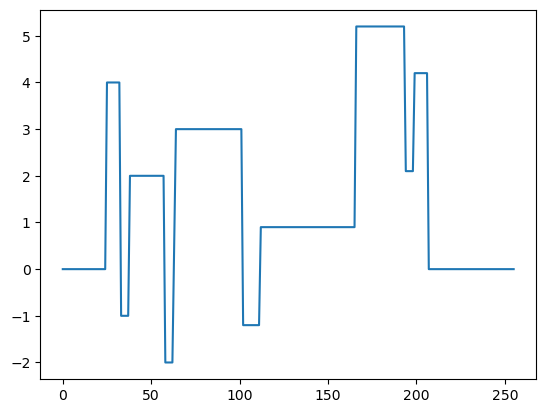
plt.plot(s)
# plt.title("original_signal")
# plt.axis('off')
[<matplotlib.lines.Line2D at 0x7f35013b3730>]
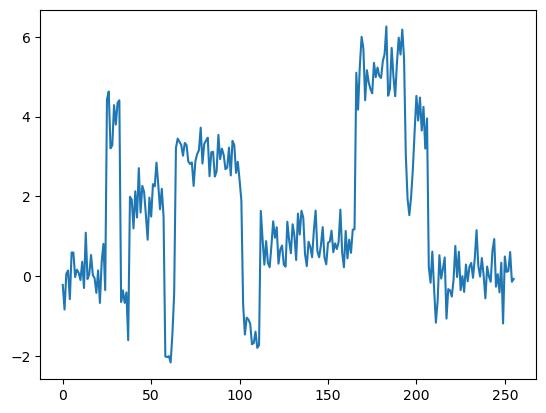
plt.plot(y)
# plt.title("noisy_signal")
# plt.axis('off')
[<matplotlib.lines.Line2D at 0x7f350132cd30>]
plt.plot(x_mm)
# plt.title("MM algorithm")
# plt.axis('off')
[<matplotlib.lines.Line2D at 0x7f35012a5310>]
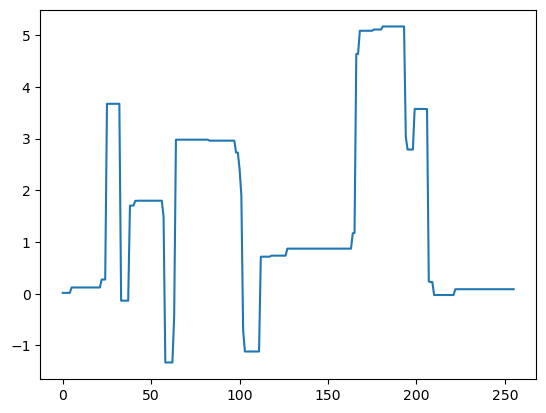
plt.plot(x_ic)
# plt.axis('off')
[<matplotlib.lines.Line2D at 0x7f3501222160>]
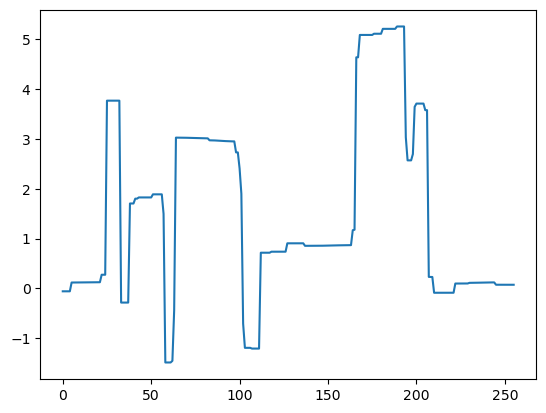
plt.plot(x_admm[::N])
# plt.axis('off')
[<matplotlib.lines.Line2D at 0x7f35012138b0>]