Compressed Sensing for MRI

Import libraries

import numpy as np
import cv2
from matplotlib import pyplot as plt
import scipy.signal as signal
from scipy.signal import convolve2d
import scipy.fft as fft
import urllib.request
from skimage.metrics import peak_signal_noise_ratio as PSNR
import time
import nibabel as nib

np.random.seed(30)

Import image

file_path = "data/0219191_mystudy-0219-1114_anat_ses-01_T1w_20190219111436_5.nii.gz"
# file_path="/content/data/dicom_examples/nii/0219191_mystudy-0219-1114_anat_ses-01_scout_20190219111436_2_i00001.nii.gz"

t1_img = nib.load(file_path)

t1_data = t1_img.get_fdata()

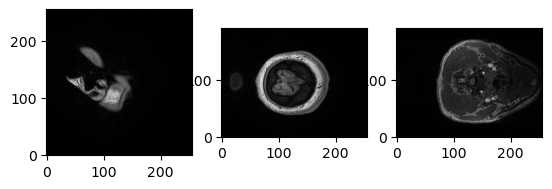
x_slice = t1_data[9, :, :]
y_slice = t1_data[:, 19, :]
z_slice = t1_data[:, :, 2]

import matplotlib.pyplot as plt

%matplotlib inline

slices = [x_slice, y_slice, z_slice]

fig, axes = plt.subplots(1, len(slices))
for i, slice in enumerate(slices):
    axes[i].imshow(slice, cmap="gray", origin="lower")

import numpy as np
import matplotlib.pyplot as plt

# Assuming x_slice, y_slice, and z_slice are the input images

slices = [x_slice, y_slice, z_slice]

# Find the maximum dimension among all images
max_dim = max(
    [slice.shape[0] for slice in slices] + [slice.shape[1] for slice in slices]
)

# Create a new list to store the padded images
padded_slices = []

# Pad zeros to make each image square
for slice in slices:
    height_diff = max_dim - slice.shape[0]
    width_diff = max_dim - slice.shape[1]
    pad_top = height_diff // 2
    pad_bottom = height_diff - pad_top
    pad_left = width_diff // 2
    pad_right = width_diff - pad_left
    padded_slice = np.pad(
        slice, ((pad_top, pad_bottom), (pad_left, pad_right)), mode="constant"
    )
    padded_slices.append(padded_slice)

# Plot the padded images
fig, axes = plt.subplots(1, len(padded_slices))
for i, slice in enumerate(padded_slices):
    axes[i].imshow(slice, cmap="gray", origin="lower")
for ax in axes.ravel():
    ax.axis("off")

Define conv and fft functions

def to_fourier_domain(x):
    return fft.fftshift(fft.fft2(fft.ifftshift(x)))


def to_image_domain(x):
    return fft.ifftshift(fft.ifft2(fft.fftshift(x)))

# Define some of the operators that we need...
def conv2d_fft(x, h):
    p0 = x.shape[0] - h.shape[0]
    p1 = x.shape[1] - h.shape[1]
    h_pad = np.pad(h, ((p0 // 2, p0 // 2), (p1 // 2, p1 // 2)))
    Fh = to_fourier_domain(h_pad)
    Fx = to_fourier_domain(x)
    return to_image_domain(Fx * Fh)


def conv2dT_fft(x, h):
    p0 = x.shape[0] - h.shape[0]
    p1 = x.shape[1] - h.shape[1]
    h_pad = np.pad(h, ((p0 // 2, p0 // 2), (p1 // 2, p1 // 2)))
    Fh = to_fourier_domain(h_pad)
    Fx = to_fourier_domain(x)
    return to_image_domain(Fx * np.conj(Fh))

Create the binary mask

According to FastMRI paper

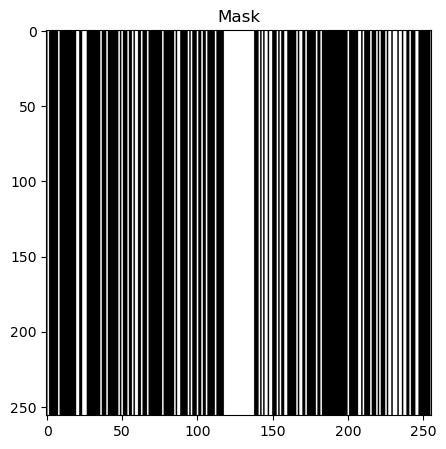
def generate_random_mask(img_shape, center_percentage=8):
    mask = np.zeros(img_shape)
    center_columns = int(img_shape[1] * center_percentage / 100)
    center_start = int(img_shape[1] / 2) - int(center_columns / 2)
    center_end = center_start + center_columns

    for col in range(center_start, center_end):
        mask[:, col] = 1

    num_random_cols = int(0.25 * img_shape[1])
    random_cols = np.random.choice(
        [i for i in range(img_shape[1]) if i < center_start or i >= center_end],
        num_random_cols,
        replace=False,
    )

    for col in random_cols:
        mask[:, col] = 1

    return mask.astype(int)

rmask = generate_random_mask(
    x_slice.shape
)  # generate a 100x100 mask with 30% center columns
# plot mask and mask_fft together
fig, axs = plt.subplots(1, 1, figsize=(10, 5))
axs.imshow(rmask, cmap="gray")
axs.set_title("Mask")
plt.show()

# assuming img_shape to be square, shape is of type (x,x) -> (512,512)
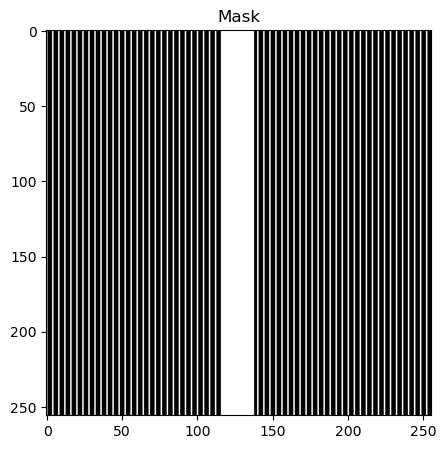
def generate_equidistant_mask(img_shape, acceleration_factor=4, center_percentage=25):
    mask = np.zeros(img_shape, dtype=np.float32)
    mask[::acceleration_factor] = 1.0

    # Set center_percentage% of the center lines to all ones
    fraction = 100 // center_percentage
    center_lines = img_shape[0] // fraction
    start = (img_shape[0] - center_lines) // 2
    end = start + center_lines
    mask[start:end] = 1.0
    return mask.T

eq_mask = generate_equidistant_mask(
    x_slice.shape, acceleration_factor=4, center_percentage=8
)
# plot mask and mask_fft together
fig, axs = plt.subplots(1, 1, figsize=(10, 5))
axs.imshow(eq_mask, cmap="gray")
axs.set_title("Mask")
plt.show()

def get_log_spectrum(fft_data):
    return 20 * np.log(np.abs(fft_data) + 1)

# Input image for processing
x = padded_slices[2]
# Equidistant Mask
eq_mask = generate_equidistant_mask(
    x.T.shape, acceleration_factor=4, center_percentage=8
)
# Random Mask
rmask = generate_random_mask(x.shape)

# Computing ploting parameters


def param(x, mask):
    spectrum_image = to_fourier_domain(x.T)
    masked_spectrum = spectrum_image * mask
    zero_filled_ifft = to_image_domain(masked_spectrum * mask)
    return spectrum_image, masked_spectrum, zero_filled_ifft


# Computing parameters for random mask and equidistant mask
spectrum_image, masked_spectrum, zero_filled_ifft = param(x, eq_mask)
spectrum_image_r, masked_spectrum_r, zero_filled_ifft_r = param(x, rmask)

fig, axs = plt.subplots(2, 5, figsize=(15, 6))
axs[0, 0].imshow(x.T, cmap="gray")
axs[0, 0].set_title("Original MRI")
axs[0, 1].imshow(eq_mask, cmap="gray")
axs[0, 1].set_title("Equidistant 4 fold Mask")
axs[0, 2].imshow(get_log_spectrum(spectrum_image), cmap="gray")
axs[0, 2].set_title("log spectrumFx")
axs[0, 3].imshow(get_log_spectrum(masked_spectrum), cmap="gray")
axs[0, 3].set_title("log spectrum MFx")
axs[0, 4].imshow(np.abs(zero_filled_ifft), cmap="gray")
axs[0, 4].set_title("zero filled ifft")
axs[1, 0].imshow(x.T, cmap="gray")
axs[1, 0].set_title("Original MRI")
axs[1, 1].imshow(rmask, cmap="gray")
axs[1, 1].set_title("Random 4-fold Mask")
axs[1, 2].imshow(get_log_spectrum(spectrum_image_r), cmap="gray")
axs[1, 2].set_title("log spectrumFx")
axs[1, 3].imshow(get_log_spectrum(masked_spectrum_r), cmap="gray")
axs[1, 3].set_title("log spectrum MFx")
axs[1, 4].imshow(np.abs(zero_filled_ifft_r), cmap="gray")
axs[1, 4].set_title("zero filled ifft")
for ax in axs.ravel():
    ax.axis("off")
plt.show()

Gradiant operator

# define gradient operators
"""
I am testing it with y1 for now
"""
dh = np.array([[1, -1], [0, 0]])  # horizontal gradient filter
dv = np.array([[1, 0], [-1, 0]])  # vertical gradient filter

Dh = lambda x: conv2d_fft(x, dh)
Dv = lambda x: conv2d_fft(x, dv)

DhT = lambda x: conv2dT_fft(x, dh)
DvT = lambda x: conv2dT_fft(x, dv)

# plot the image x and the gradient images Dh x and Dv x
fig = plt.figure(figsize=(15, 15))
plt.subplot(131)
plt.imshow(x.T, cmap="gray")
plt.title("image x")
plt.subplot(132)
plt.imshow(np.abs(Dh(x.T)), cmap="gray")
plt.title(r"$|D_hx|$")
plt.subplot(133)
plt.imshow(np.abs(Dv(x.T)), cmap="gray")
plt.title(r"$|D_vx|$")
plt.tight_layout()
plt.show()

TV Primal Dual

TV Compress Sensing MRI using Primal Dual

def TV_MRI(MFx, M, lamb=2, maxiter=50, tol=1e-4):
    """
    TV-Compress Senssing MRI solver to solve
    minimize 0.5 |z-Hx|_2^2 + lambda|Dx|_1
    z : reconstructed img in each update
    x : original image
    Hx: masked image
    """
    start = time.time()
    # define the soft-thresholding function
    soft_thresh = lambda v, t: np.maximum(np.abs(v) - t, 0.0) * np.sign(v)

    # set step-sizes at maximum: τσL² < 1
    # note: PDS seems sensitive to these (given finite iterations at least...)
    L = np.sqrt(8)  # Spectral norm of D
    tao = 0.99 / L
    sigma = 0.99 / L

    # Defining Prox functions
    """
  z^k+1 = prox_tg(z^k-tD^Ty^k) 
  y^k+1 = prox_sigmaf*(y^k+sigmaDx^k+1)
  """
    # Proximal Gradient Descent on x (primal)
    prox_D = lambda v, z: to_image_domain(
        (to_fourier_domain(v) + tao * z) / (1 + tao * M)
    )
    # Proximal Gradient Ascent on z (dual)
    # prox_A = lambda v: (v - sigma*soft_thresh(v/sigma, lamb/sigma))
    prox_A = lambda v: np.clip(v, -lamb, lamb)

    # -----------------------------
    # initilize iteration variables
    z_hat = np.zeros_like(MFx)
    yh_hat = np.zeros_like(MFx)
    yv_hat = np.zeros_like(MFx)
    # For computing error
    J = np.zeros(maxiter)

    # Iterations
    k = 0
    while k < maxiter:
        # Update x - ProxD
        z_old = z_hat
        z_hat = prox_D(z_hat - tao * (DhT(yh_hat) + DvT(yv_hat)), MFx)
        # Update y - ProxA
        yh_hat = prox_A(yh_hat + sigma * (Dh(2 * z_hat - z_old)))
        yv_hat = prox_A(yv_hat + sigma * (Dv(2 * z_hat - z_old)))
        # compute the convergence

        # dual_h = Dh(z_hat) - yh_hat
        # dual_v = Dv(z_hat) - yv_hat
        # J[k] = (dual_h**2).sum()+(dual_v**2).sum()
        J[k] = np.abs(z_hat - z_old).sum()
        if J[k] < tol:
            break
        k = k + 1

    end = time.time()
    return z_hat, J, end - start

x_t, j, duration1 = TV_MRI(masked_spectrum, eq_mask, lamb=5, maxiter=500, tol=1e-2)
x_t_ifft = to_image_domain(x_t)
fig = plt.figure()
fig.set_size_inches(5, 7.5)
ax = fig.add_subplot(321)
ax.imshow(x.T, cmap="gray")
plt.title("original image")
ax2 = fig.add_subplot(322)
ax2.imshow(np.abs(zero_filled_ifft), cmap="gray")
plt.title("Corrupted image")
ax3 = fig.add_subplot(323)
ax3.imshow(np.abs(x_t), cmap="gray")
plt.title("recovered image")
ax4 = fig.add_subplot(324)
ax4.semilogy(range(len(j)), j, "b-", lw=2)
plt.title("Residual")
plt.xlabel("iteration (k)")
plt.tight_layout()
plt.show()
print(f"Time taken = {duration1}")

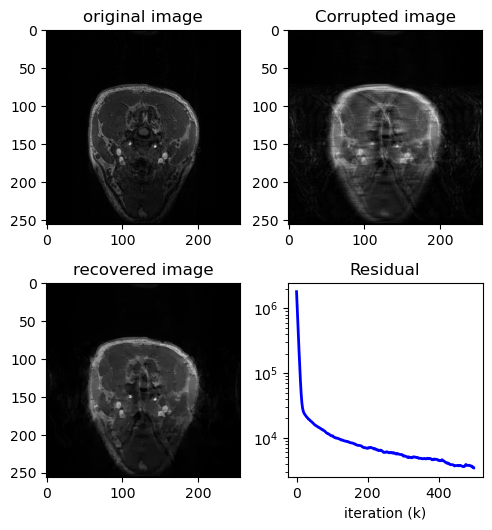
Time taken = 7.693760633468628

PSNR(x.T, np.abs(zero_filled_ifft), data_range=np.max(np.abs(x)))

28.910346296010466

PSNR(x.T, np.abs(x_t), data_range=np.max(np.abs(x)))

31.11096519230359

x_tr, jr, duration1r = TV_MRI(masked_spectrum_r, rmask, lamb=5, maxiter=500, tol=1e-2)

fig = plt.figure()
fig.set_size_inches(5, 7.5)
ax = fig.add_subplot(321)
ax.imshow(x.T, cmap="gray")
plt.title("original image")
ax2 = fig.add_subplot(322)
ax2.imshow(np.abs(zero_filled_ifft_r), cmap="gray")
plt.title("Corrupted image")
ax3 = fig.add_subplot(323)
ax3.imshow(np.abs(x_tr), cmap="gray")
plt.title("recovered image")
ax4 = fig.add_subplot(324)
ax4.semilogy(range(len(jr)), jr, "b-", lw=2)
plt.title("Residual")
plt.xlabel("iteration (k)")
plt.tight_layout()
plt.show()
print(f"Time taken = {duration1r}")

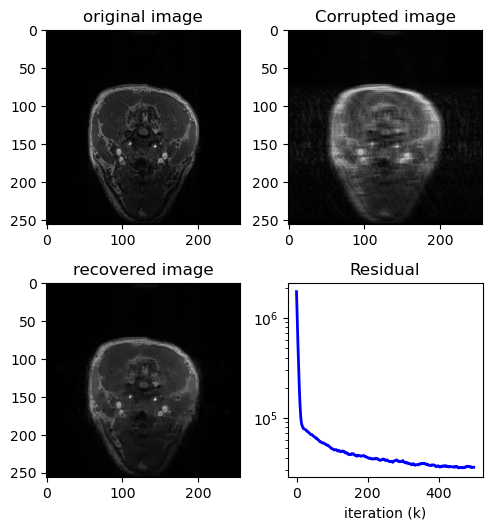
Time taken = 7.645873546600342

PSNR(x.T, np.abs(zero_filled_ifft_r), data_range=np.max(np.abs(x)))

28.999801885609365

PSNR(x.T, np.abs(x_tr), data_range=np.max(np.abs(x)))

33.28850707391314

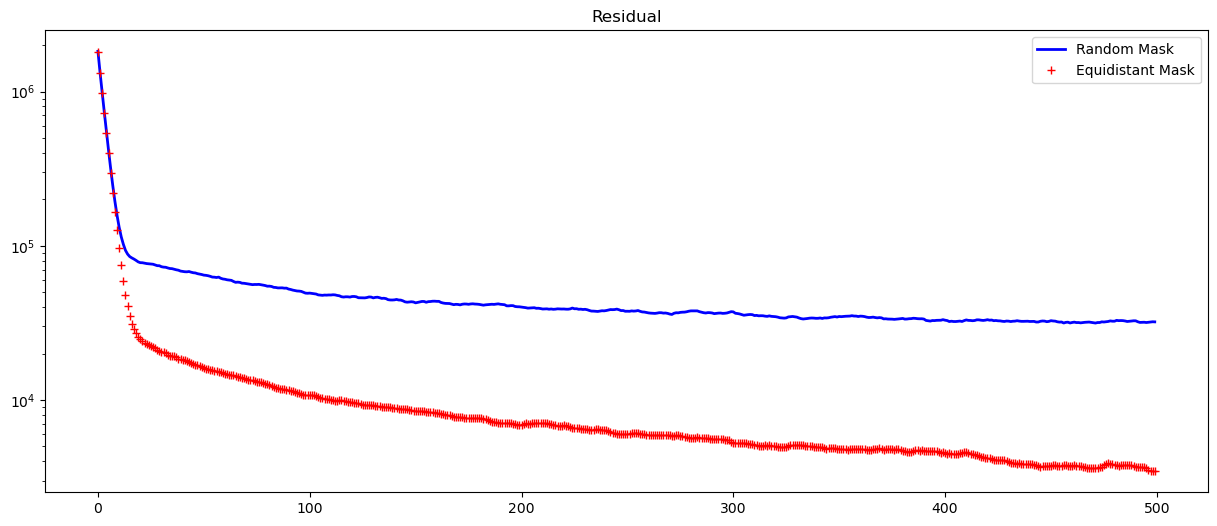
fig, axs = plt.subplots(1, 1, figsize=(15, 6))
axs.semilogy(range(len(jr)), jr, "b-", lw=2, label="Random Mask")
axs.semilogy(range(len(j)), j, "r+", lw=2, label="Equidistant Mask")
plt.title("Residual")
plt.legend()

<matplotlib.legend.Legend at 0x7f3062d97850>